【印刷可能】 f(x y z x^2 y^2 z^2)=0 803648-F x y z x 2 y 2 z 2 0

If $ u=f(xy,yz,zx) , $ then show that $ \dfrac{\partial u}{\partial x} \dfrac{\partial u}{\partial y} \dfrac{\partial u}{\partial z} \;=\;The random variable X is the number of heads in these 10 tosses, and Y is the number of heads in the first 3 tosses In spite of the fact that Y emerges before X it may happen that Sadece x ve y değişkenleri ile sorulmuş olsaydı çözebilirdim sürekli olduğunu gösterme tanımından ancak z olunca kitlendim ( 8, Aralık, 15 komkesersedat ( 24

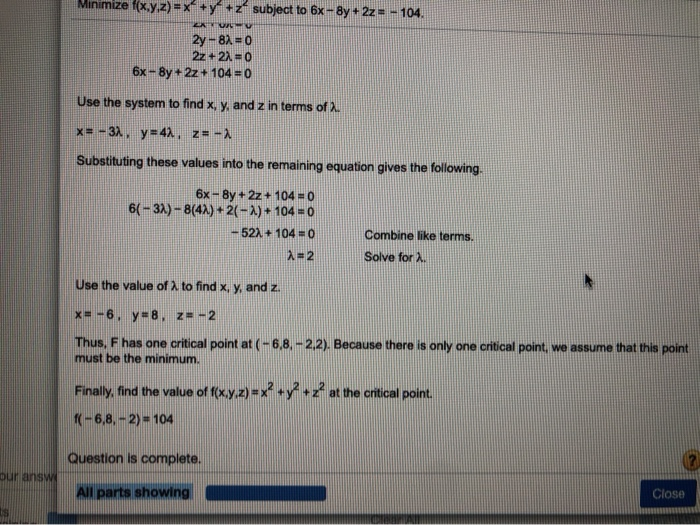
Solved Minimize F X Y Z X2 Y2 Z Subject To 8x 2y Chegg Com

F x y z x 2 y 2 z 2 0

F x y z x 2 y 2 z 2 0-Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorT e Depiction of a twodimensional vector field with a uniform curl In vector calculus, the curl is a vector operator that describes the infinitesimal circulation of a vector field in threedimensional Euclidean space The curl at a point in the field is represented by a vector whose length and direction denote the magnitude and axis of the

10 Points Uae The Lagrange Multiplletsfincl Che Abs Itprospt

(xyz)(xzxyyz)xyz Final result x2y x2z xy2 2xyz xz2 y2z yz2 Step by step solution Step 1 Equation at the end of step 1 (x y z xyz=1, find max of x^2yy^2zz^2x you may think x=y=z=\dfrac{1}{3} is the point of max, but the real one is x=\dfrac{2}{3},y=\dfrac{1}{3},z=0 or Difficult equations to rewrite as3) Solve the equation x 2 25 = 0 Solution x 2 25 = (x 5)(x 5) => we have to solve the following 2 equations x 5 = 0 or x 5 = 0 so the equation have two decisions x = 5 and x = 5 Related Resources Polynomial identities quiz Simplifying polynomial expressions problems with solutions Factoring polynomials problems withZ 2 0 (12r3 − 3r5)dr = 32π (b) F(x,y,z) = (x 2 sin(yz))i (y − xe−z)j z k;

Z ∞ −∞ f(x,y)dydx = Z 1 0 Z 2 0 (cx2 xy 3)dydx = 2c 3 1 3, so c = 1 (b) Draw a picture of the support set (a 1by2 rectangle), and intersect it with the set {(x,y) x y ≥ 1}, which is the region above the line y = 1 − x See figure above, right To compute the probability, we double integrate the joint density over this30k • modified 22 years ago engineering mathematics ADD COMMENT FOLLOW SHARE EDIT 1Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science

Conditioning on the discrete level Example A fair coin is tossed 10 times; How do you find the maximum value of the function #f(x,y,z)= x2y3z# subject to the constraint #z=4x^2y^2#?The three loci of double points x = 0, y = 0, and z = 0, intersect at a triple point at the origin For example, given x = yz and y = zx, the second paraboloid is equivalent to x = y / z Then and either y = 0 or z2 = 1 so that z = ±1 Their two external intersections are x = y, z = 1;

Solved Verify That The Divergence Theorem Is True For The Chegg Com

Solved Consider The Vector Function F X Y Z E X Sin Y Z Y E X Cos Y Xz Y 2 X Y 1 Z A

 The gradient is = The gradient is a vector gradf=((delf)/(delx), (delf)/(dely), (delf)/(delz)) f(x,y,z)=3x^2yy^3z^2 (delf)/(delx)=6xy (delf)/(delyPlot z=x^2y^2 Natural Language; 2x2yz = 1 First we rearrange the equation of the surface into the form f(x,y,z)=0 z=x^22xyy^2 x^22xyy^2z = 0 And so we define our surface function, f, by f(x,y,z) = x^22xyy^2z In order to find the normal at any particular point in vector space we use the Del, or gradient operator grad f(x,y,z) = (partial f)/(partial x) hat(i) (partial f)/(partial y) hat(j)

Example 15 If X Y Z Are Different Show 1 Xyz 0 Class 12

2 3 Tangent Plane To A Surface Mathematics Libretexts

Y(0)=0 3 Comments Show Hide 2 older comments Walter Roberson onExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition So substituting the values for the elementary symmetric polynomials that we found, we find that x, y and z are the three roots of t3 −t2 − 1 2t − 1 6 = 0 or if you prefer 6t3 − 6t2 −3t −1 = 0 In theory we could solve this using Cardano's method and directly evaluate x4 y4 z4, but the methods used above are somewhat easier

15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts

Find The Maximum Value Of X Y Z When Ax By Cz P Quora

F2 (x, y, z) = 2x^2 y^2 − 4z = 0 f3 (x,y,z) = 3x^2 −4yz^2 = 0 This system can be concisely represented as F (x) = 0, where F (x) = (f1, f2, f3)T , x= (x,y,z)T and 0 = (0,0,0)T (transpose written because these should be column vectors) Using matlab Starting with the initial condition x0 = (05, 05, 05)T , implement two steps ofFirst week only $499!The solution (x,y,z) = (0,1,1) works for all n If you don't want to allow 0, then let x,y ∈ N be such that xyi = (12i)n Then 5n = ((1 2i)(1−2i))n = (1 2i)n(1−2i)n = (xyi)(x −yi) = x2 y2 Find all natural solutions to x2 2y2 = z2 duplicate https//mathstackexchangecom/q/

Solve A System Of Non Linear Equation Docx

Multivariable Calculus Using Nabla With Partial Derivatives And The Laplace Operation Partial X 2 Partial Y 2 Partial Z 2 Mathematics Stack Exchange

Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, scienceTreating S as a x simple region, we have for fixed y − z, x going from 0 to q 1− y2 9 − z2 4 The projected region in the y−z plane can be described as a zsimple region in the y − z plane and described by ((y,z) 0 ≤ z ≤ 2 r 1− y2 9,0 ≤ y ≤ 3) So, the above integral is the same as Z 3 0 Z 2 q 1−y 2 9 0 Z q 1−y 2 9 −Let f(x,y,z) = x2 2y2 3z2 The normal vector of the plane 3x − 2y 3z = 1 is h3,−2,3i The normal vector for tangent plane at the point (x 0,y 0,z 0) on the ellipsoid is ∇f(x 0,y 0,z 0) = h2x 0,4y 0,6z 0i Since the tangent plane is parallel to the given plane, ∇f(x 0,y 0,z 0) = h2x 0,4y 0,6z 0i = ch3,−2,3i or hx 0,2y 0,3z 0i

Solved In Exercises 5 16 Use The Divergence Theorem To Chegg Com

15 5 The Chain Rule

Soluciones de problemas de Cálculo (grupo D 15/16) 2 Cálculo diferencial en Rn 1 f(x;y)= e3xx4y2 f x =(34x2y2)e3xx 4y2, f y =2x4ye3xx 4y2 8(x;y) g(x;y)= log y x2 g x = 2x x2y, g y = 1 yx2,si y,x2 (enesospuntosniestádefinida) h(x;y)= 1 xy sen(xy) h(x;0)=h(0;y)=1 Si x,0, y,0,es h x = 1 x cos(xy) 1 x 2y sen(xy), hYou can solve this without really using any formulas, but rather by means of words and common sense The formula for cost of production c = 025x basically tells you this first you pay \ $0 to set things up Rent the building, put up a sign at the entrance, etc Then, after this, you pay \$ More Items Copied to clipboard  x3y4z = 0 First we rearrange the equation of the surface into the form f(x,y,z)=0 x^22z^2 = y^2 x^2 y^2 2z^2 = 0 And so we have our function f(x,y,z) = x^2 y^2 2z^2 In order to find the normal at any particular point in vector space we use the Del, or gradient operator grad f(x,y,z) = (partial f)/(partial x) hat(i) (partial

2

12 6 Quadric Surfaces Mathematics Libretexts

S is the surface of the region bounded by the cylinder x2 y2 = 4 and the planes x z = 2 and z = 0 Solution The divergence of F is divF = ∂ ∂x (x2 sin(yz)) ∂ ∂y (y − xe−z) ∂ ∂z (z2) = 2x 12z Let E be the region {(x,y,z) 0 ≤ zX = − y, z = −1When x = 0 this becomes f = y2, a parabola in the yz plane;

1 9 3 We Would Like To Make The Length 6 The Only Vectors In The Same Direction As V Are Those Pdf Free Download

Homework Assignment 4 Math 253

Again, letz=f(x;y) be a function ofxandy 2z @x2 means the second derivative with respect toxholdingyconstant 2z @y2 means the second derivative with respect toyholdingxconstant 2z @x@ymeans difierentiate flrst with respect toyand then with respect tox The \mixed" partial derivative@ 2z @x@yis as important in applications as the othersCalculus Graphing with the First Derivative Identifying Stationary Points (Critical Points) for a FunctionCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history

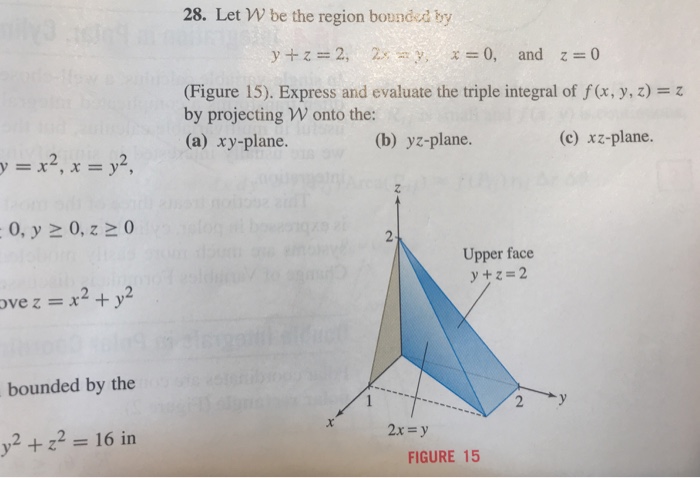
Solved 28 Let W Be The Region Bounded By Y Z 2 2x Y X 0 Chegg Com

Systems Engineering And Analysis Ppt Download

 Ex 42, 9 Chapter 4 Class 12 Determinants (Term 1) Last updated at by Teachoo Introducing your new favourite teacher Teachoo Black, at only ₹ per month Join Teachoo Black Next Ex 42, 10 (i) → Chapter 4 Class 12 Determinants;X^2 y^2 z^2 = 1 Natural Language;Subtracting the equations in pairs we get (x−y)(xy z) = 0 (x− z)(xy z) = 0 (y −z)(x yz) = 0 If x y z = 0 then x = y = z, but then x2 − yz = 0 = i so we must have x y z = 0 More Items

Calc 501 1000 By James Bardo Issuu

Geometry Verify Stokes Theorem For V Zi Xj Yk Over The Hemispherical Surface X 2 Y 2 Z 2 1 And Z Gt 0 Mathematics Stack Exchange

42 Conditional Distributions and Independence Definition 421 Let (X,Y) be a discrete bivariate random vector with joint pmf f(x,y) andmarginal pmfs fX(x) and fY (y)For any x such that P(X = x) = fX(x) > 0, the conditional pmf of Y given that X = x is the function of y denoted by f(yx) and defined by f(yx) = P(Y = yX = x) = f(x,y) fX(x) For any y such that P(Y = y) = fY (y) > 0, the how can i draw graph of z^2=x^2y^2 on matlab Learn more about surface MATLAB C/C Graphics Library Skip to content Toggle Main Navigation Sign In to Your MathWorks Account Sign In to Your MathWorks Account;When y = 0 we get the "same" parabola f = x2 in the xz plane Now consider the line y = kx If we simply replace y by kx we get f(x,y) = (1 k2)x2 which is a parabola, but it does not really "represent" the crosssection along y =

Divergence Theorem F X Y Z Xye X I Xy 2z 3 J Ye Z K S Is The Surface Coordinate Planes Youtube

Example 32 Show That Determinant 2xyz X Y Z 3 Class 12

0 $ written 60 years ago by teamques10 ★Find stepbystep solutions and your answer to the following textbook question Let F(x, y, z) = xi yj zk, and let f(x, y, z) = ǁF(x, y, z)ǁ (a) Show that ∇(ln f) = F/f² (b) Show that ∇(1/f) = F/f³ (c) Show that $$ ∇f^n = nf^{n2} F $$ (d) The Laplacian is the differential operator ∇² = ∇·∇ = ∂²/∂x² ∂²/∂y² ∂²/∂z² and Laplace's equation is ∇Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science

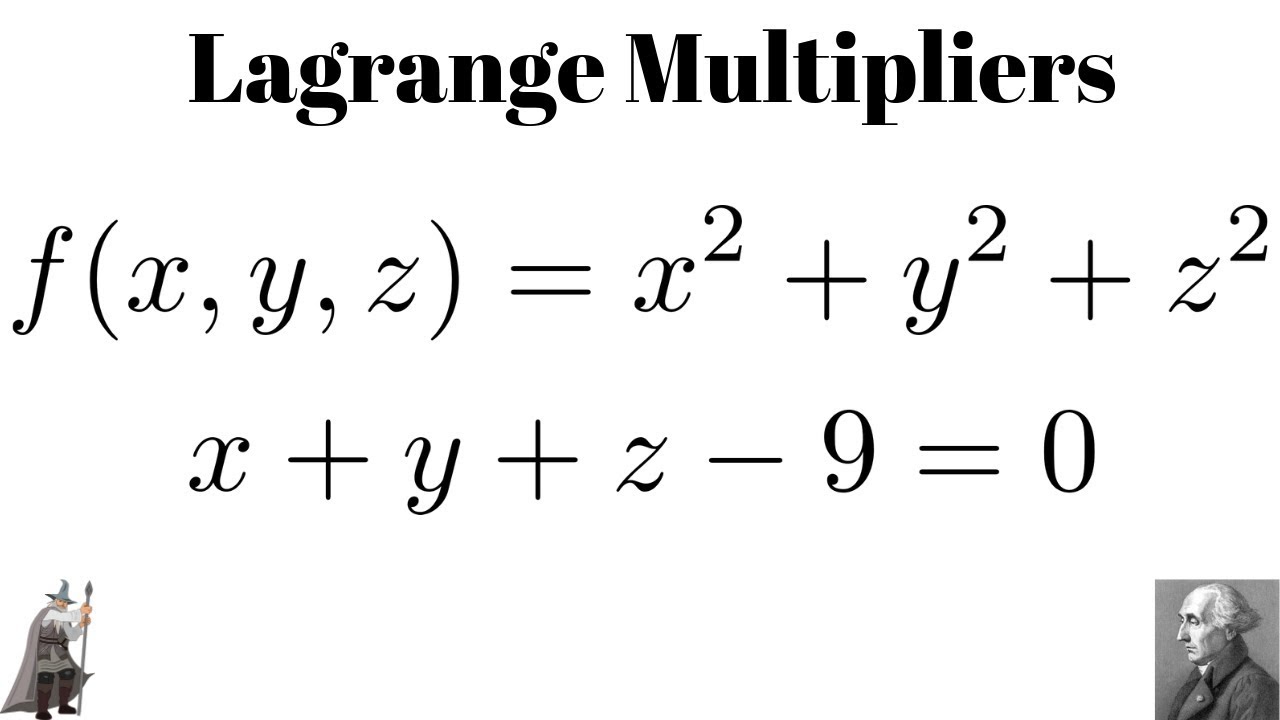
Lagrange Multipliers Minimum Of F X Y Z X 2 Y 2 Z 2 Subject To X Y Z 9 0 Youtube

Calc 501 1000 By James Bardo Issuu

Click HERE to return to the list of problems SOLUTION 14 Begin with x2/3 y2/3 = 8 Differentiate both sides of the equation, getting (Remember to use the chain rule on D ( y2/3 ) ) so that (Now solve for y ' ) Since lines tangent to the graph will have slope $ 1 $ , set y ' =Example 5422 Find the directional derivative of f(x,y,z)= p xyz in the direction of ~ v = h1,2,2i at the point (3,2,6) First, we find the partial derivatives to define the gradient fx(x,y,z)= yz 2 p xyz fy(x,y,z)= xz 2 p xyz fz(x,y,z)= xy 2 p xyz The gradient is rf(3,2,6) = ⌧ 12 2(6), 18 2(6), 6 2(6) = ⌧ 1, 3 2, 1 2 = 1 2 h2,3,1i 118Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields It only takes a minute to sign up

Surfaces Part 2

15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts

Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and morePlot f(x,y,z)=x^2y^2z^2 Natural Language;Midterm 2 Sample question solutions Math 125BWinter13 1 Suppose that f R3 → R2 is defined by f(x,y,z) = x2 yz,sin(xyz) z (a) Why is f differentiable on R3?Compute the Jacobian matrix of f

How To Prove That Math X Y Z 3 27xyz Geq0 Math Quora

1

Vyriešte matematické problémy pomocou nášho bezplatného matematického nástroja, ktorý vás prevedie jednotlivými krokmi riešení Podporované sú základné matematické funkcie, základná aj pokročilejšia algebra, trigonometria, matematická analýza a ďalšie oblastiArrow_forward learn write Find the flux of F = yi 2zxj – z²k through the parabolic cylinder y = x2,0 < x < 1,0 < z< 4, in162 Line Integrals We have so far integrated "over'' intervals, areas, and volumes with single, double, and triple integrals We now investigate integration over or "along'' a curve—"line integrals'' are really "curve integrals'' As with other integrals, a geometric example may be easiest to understand Consider the function f = x y and

2

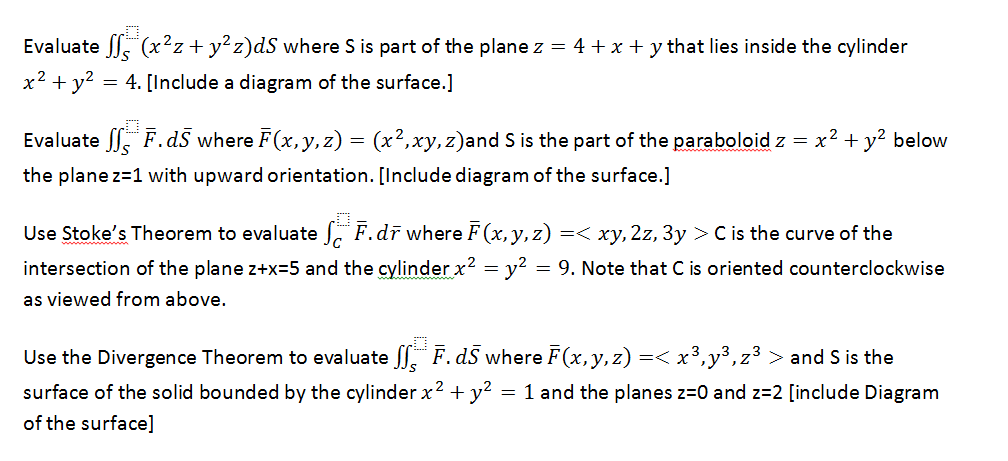
Solved Evaluate X2z Y2z Ds Where S Is Part Of The Plane Chegg Com

In mathematics, function composition is an operation ∘ that takes two functions f and g, and produces a function h = g ∘ f such that h(x) = g(f(x))In this operation, the function g is applied to the result of applying the function f to xThat is, the functions f X → Y and g Y → Z are composed to yield a function that maps x in domain X to g(f(x)) in codomain ZEECS 31/CSE 31/ICS 151 Homework 2 Questions with Solutions View Questions Only View Questions with Strategies Problem 1 Question (Theorems of Boolean algebra) Give proofs to the following theoremsSolution for Find the flux of F¯ = (x − y)i xj across the circle x 2 y 2 = 4 in the xyplane Skip to main content close Start your trial now!

Calculus Find Max And Min With Lagrange Multipliers F X Y Z Xyz 2 G X Y Z X 2 Y 2 Z 2 1 0 Mathematics Stack Exchange

Solved Find The Extreme Value Of The Function Subject To The Chegg Com

After you enter the expression, Algebra Calculator will plug x=6 in for the equation 2x3=15 2(6)3 = 15 The calculator prints "True" to let you know that the answer is right More Examples Here are more examples of how to check your answers with Algebra Calculator Feel free to try them now For x6=2x3, check (correct) solution x=3 x6=2xCartesian coordinate system with a circle of radius 2 centered at the origin marked in red The equation of a circle is (x − a)2 (y − b)2 = r2 where a and b are the coordinates of the center (a, b) and r is the radius The invention of Cartesian coordinates in the 17th century by René Descartes ( Latinized name Cartesius) revolutionizedSo for question 38 we're looking to minimize the function F, which is given as f of X y z is equal Thio X squared plus y squared plus C squared And then now we are given the constraints Um, X plus two I was three z equal six and expose three way place nine z is equal to nine

Surfaces Part 2

Exercise 5 2 4 Finding The Difference Between Two Boo Itprospt

Z = 8 − 3 x 2 − 2 y 2 = f (x, y) \\begin{equation} z = 8 3 x ^ { 2 } 2 y ^ { 2 } = f ( x , y ) \\end{equation} z = 8 − 3 x 2 − 2 y 2 = f (x, y) The tangent plane to z z z at a given point P 0 (x 0, y 0, z 0) P _ { 0 } \\left( x _ { 0 } , y _ { 0 } , z _ { 0 } \\right) P 0 (x 0 , y 0 , z 0 ) is given by

Geometry Verify Stokes Theorem For V Zi Xj Yk Over The Hemispherical Surface X 2 Y 2 Z 2 1 And Z Gt 0 Mathematics Stack Exchange

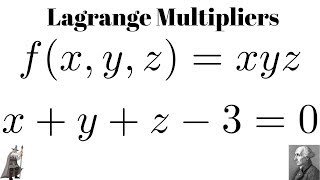
Lagrange Multipliers Maximum Of F X Y Z Xyz Subject To X Y Z 3 0 Youtube

Points Of Intersection Between Implicit F X Y Z 0 And Explicit Z Z X Y Surfaces Geogebra

Linear Algebra Sheet 5 Summer 19 Warning Popup Annotation Has A Missing Or Invalid Parent Studocu

How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora

Functions Of Several Variables 13 Copyright C Cengage Learning All Rights Reserved Ppt Download

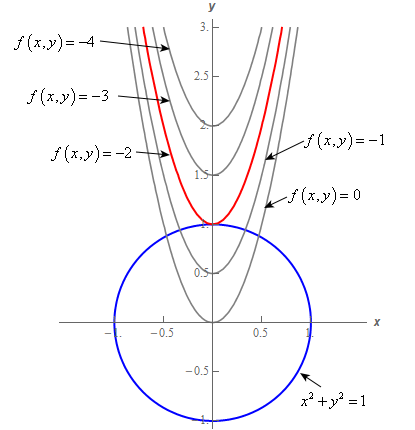
Calculus Iii Lagrange Multipliers

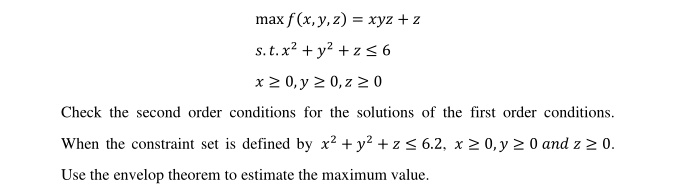
Max F X Y Z Xyz S T X2 Y2 Z 6x Y 2 0 Itprospt

Analytic Geometry Find The Equation Of The Plane That Passes Through The Line Of Intersection Of The Planes Mathematics Stack Exchange

A A Scalar Field Is Defined Byf X Y 2 Xyz Xyl Yz Itprospt

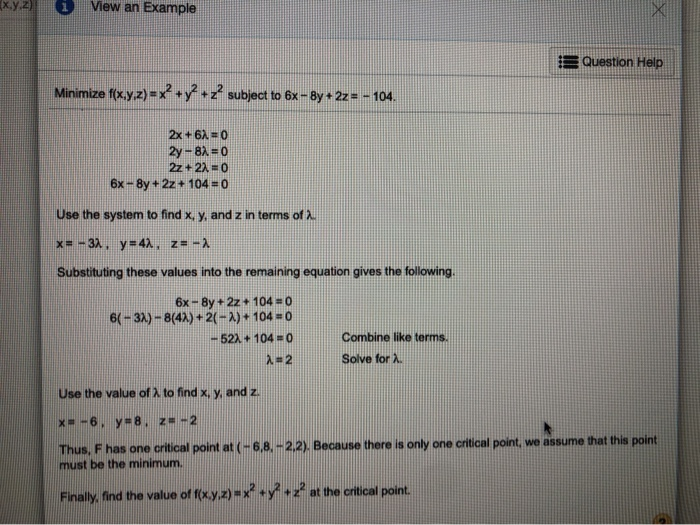
Solved Minimize F X Y Z X2 Y2 Z Subject To 8x 2y Chegg Com

Lagrange Multipliers Ppt Download

Oneclass 3 2 6 Use Stokes Theorem To Evaluate Is Curl F Ds 2 F X Y Z X2 Sin Z I Y 2 J X

Solved Let F X Y Z X Y 2 Sin Xyz And Let P 2 0 1 A Find The Equation Of The Tangent Plane To The Surface F X Y 2 3 At P B Find The Directions Unit Vectors Perpendicular To I

10 Points Uae The Lagrange Multiplletsfincl Che Abs Itprospt

15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts

Example 15 If X Y Z Are Different Show 1 Xyz 0 Class 12

Solved Minimize F X Y Z X2 Y2 Z Subject To 8x 2y Chegg Com

Example 15 If X Y Z Are Different Show 1 Xyz 0 Class 12

Geometry Verify Stokes Theorem For V Zi Xj Yk Over The Hemispherical Surface X 2 Y 2 Z 2 1 And Z Gt 0 Mathematics Stack Exchange

How To Do Implicit Differentiation 7 Steps With Pictures

Multivariable Calculus Prove That The Cone S X Y Z In b R 3 X 2 Y 2 Z 2 0 Is Not A Smooth Surface Mathematics Stack Exchange

Matlab Tutorial

Example 32 Show That Determinant 2xyz X Y Z 3 Class 12

Evaluatef X Y Z Ds F X Y Z X2 Y2 Z2 Itprospt

Solutions For Review Problems

Math 6c Chapter 12 Quiz

Solved B Suppose F X Y Z Xyz Y Z 2 Given X Chegg Com

Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z

The Divergence Of A Vector Field Youtube

2

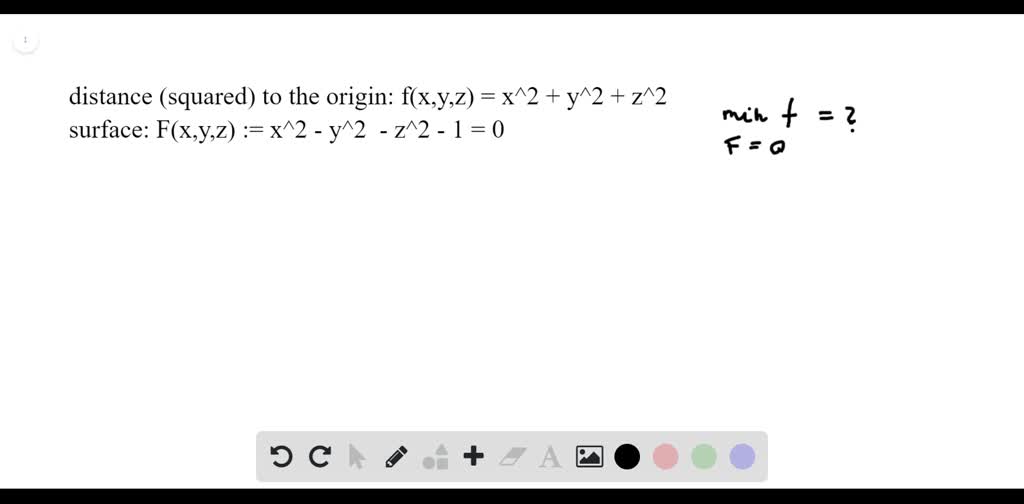
Solved Minimum Distance To The Origin Find The Minimum Distance From The Surface X 2 Y 2 Z 2 1 To The Origin

Lagrange Multipliers By Rohit Venkat Ppt Video Online Download

Solved Find The Extreme Values Of F X Y Z X 2 Y Z 1 On The Intersection Of The Plane Z 1 With The Sphere X 2 Y 2 Z 2 10

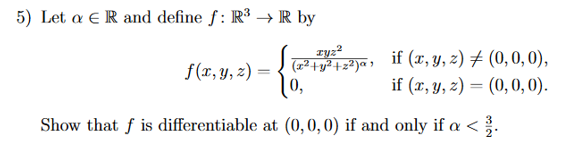
Solved Let F X Y Z Xyz 2 X 2 Y 2 Z 2 A If X Y Z Chegg Com

2

Solved 1 Consider The Function F R Rgiven By Log X2 Chegg Com

2

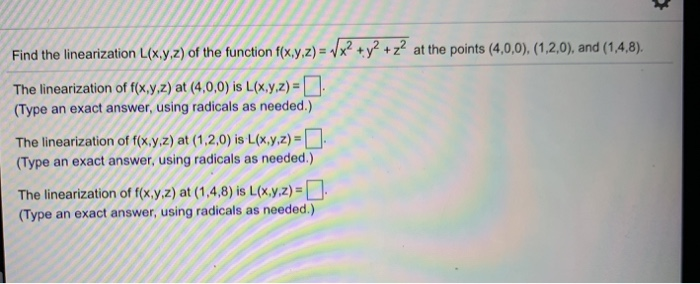
Solved Find The Linearization L X Y Z Of The Function Chegg Com

Solved Find The Total Derivative Of F X Y Z X2 Y2 Chegg Com

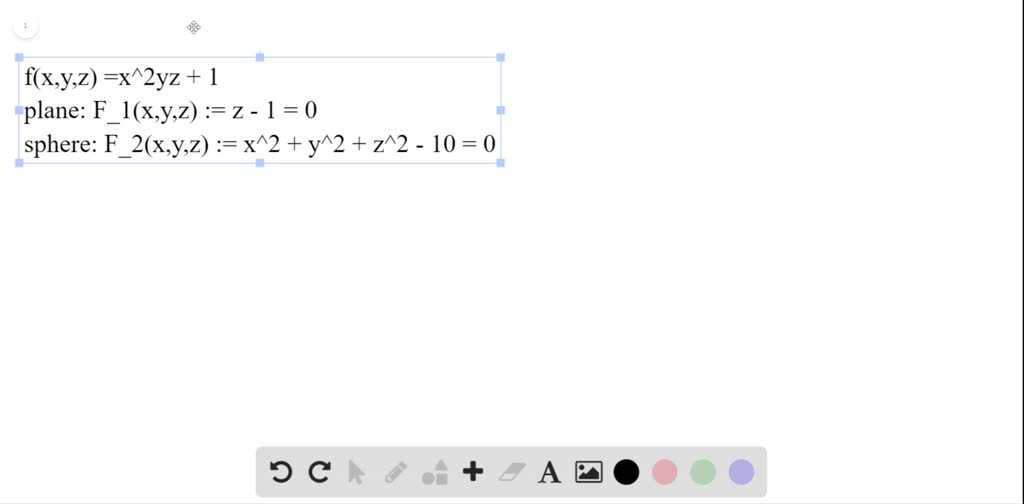
Solved Find The Extreme Values Of F Xy 2 X2yz On The Intersection Of The Plane Z 3 With The Sphere Y2 22 18

Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5

2

Solved For The Following Exercises Use The Method Lagrange Multipliers T0 Find The Maximum And Minimum Values Of The Function Subject To The Given Constraints 358 Fkx Y Xyx 2y2 6 359 F X Y 2

Section 14 7 Surface Integrals

1 Point Suppose That F X Y Z Xlyz Xyz Is A Fun Itprospt

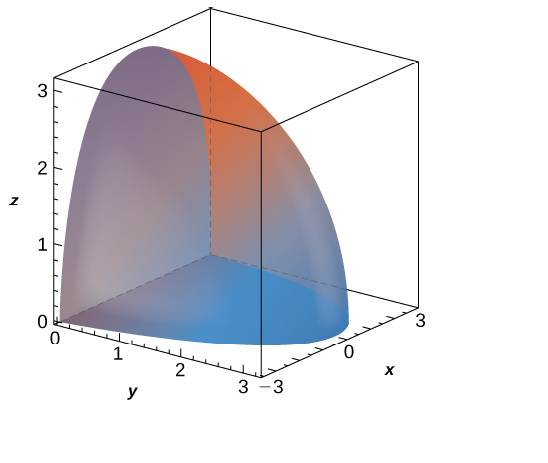
270 F X Y Z 1 X 2 Y 2 Z 2 B X Y Z X 2 Y 2 Z 2 9 Y 0 Z 0 Bartleby

Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z

Functions Of Several Variables Ppt Download

Geometry Verify Stokes Theorem For V Zi Xj Yk Over The Hemispherical Surface X 2 Y 2 Z 2 1 And Z Gt 0 Mathematics Stack Exchange

2

Lagrange Method Formula

Example 32 Show That Determinant 2xyz X Y Z 3 Class 12

1

Math 0240 Review For Final Exam 1 Let F X Y Z X 2yz Y 3z X

Matlab Tutorial

32 Approximation Of Eg6 Shrek F X Y Z X 4 Y 4 Z 4 4 X 2 Download Scientific Diagram

Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z

Conf Math Illinois Edu

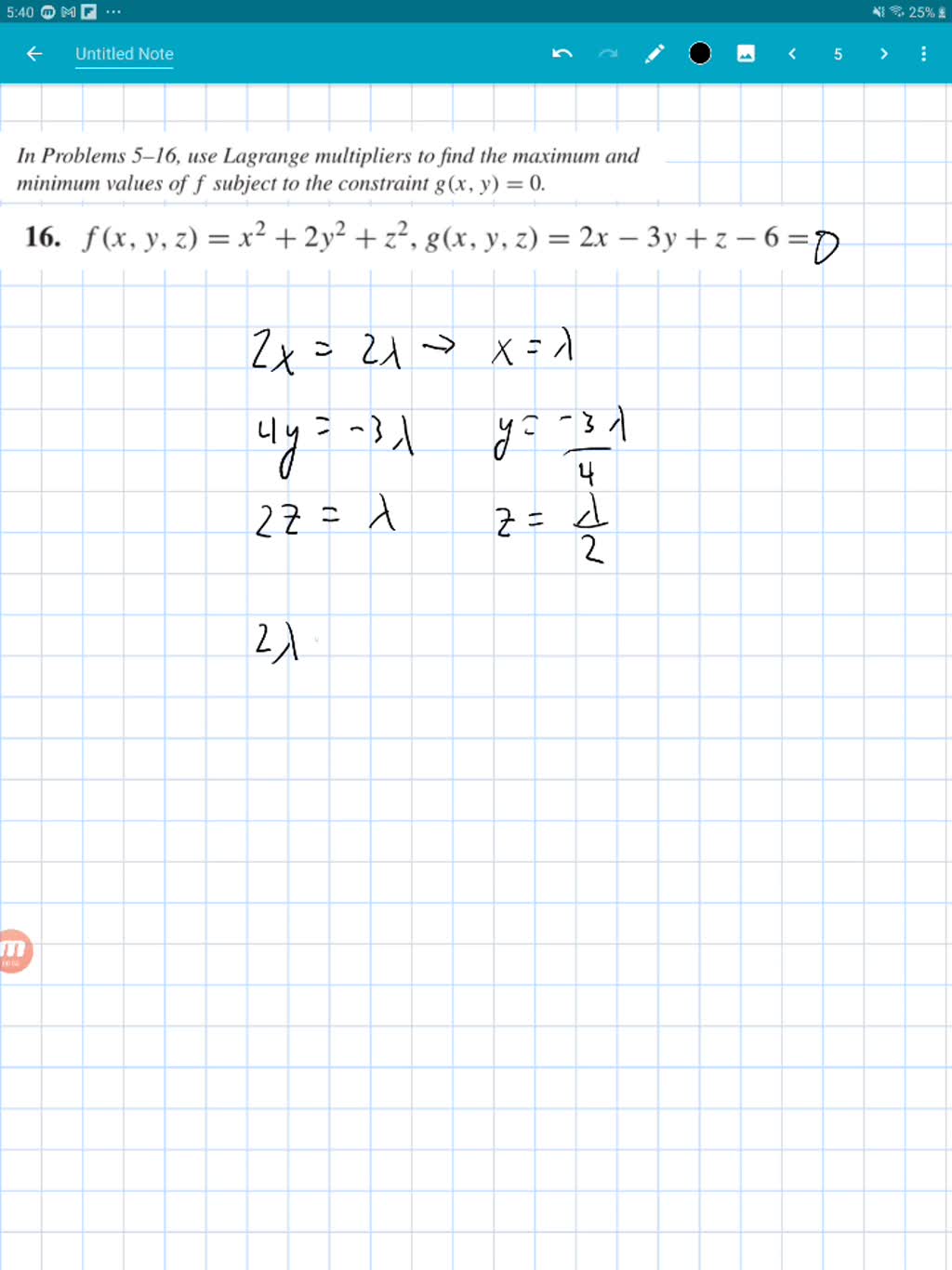
Max F X Y Z Xyz S T X2 Y2 Z 6x Y 2 0 Itprospt

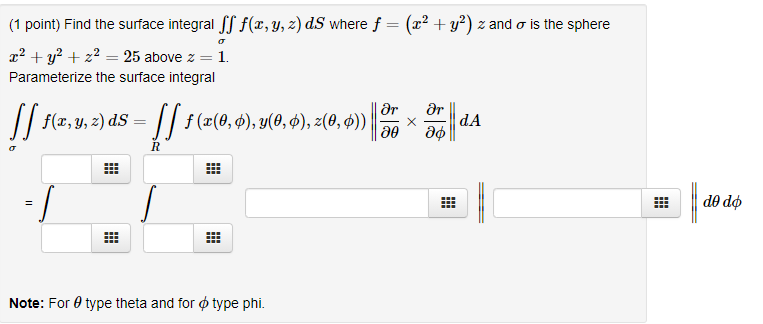
Solved 1 Point Find The Surface Integral Chegg Com

Solutions To Homework Assignment 4 Math Pdf Free Download

Answered 3j 8 F X Y Xin Y P 3 1 U 5 13 Bartleby

Incoming Term: f x y z x 2 y 2 z 2 0, f x y z x 2 y 2 z 2 0 pde,